| Time | Dec 2, 2022, 10:00 am (Taipei Time) |
| Speaker | Ming-Chien Hsu |
| Title | Quantum state tomography via non-convex Riemannian gradient descent |
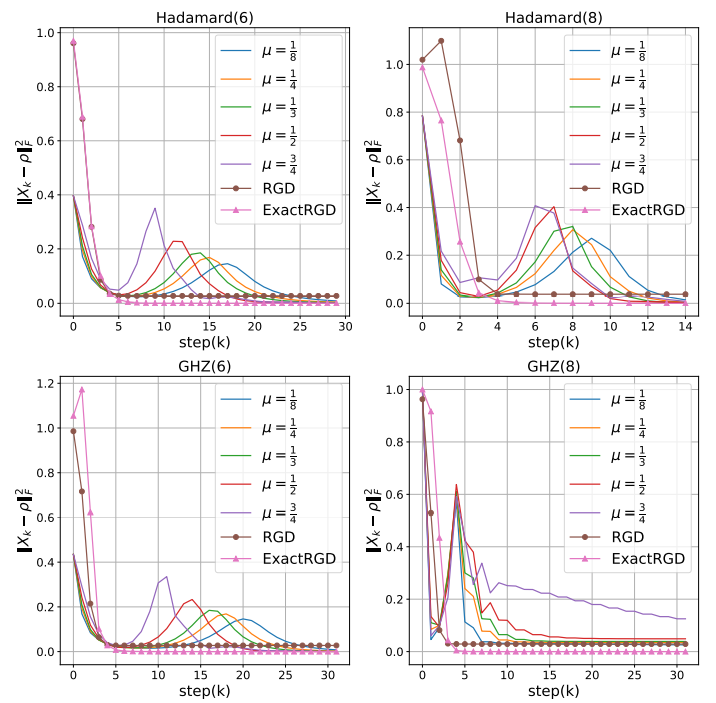
| Abstract | The recovery of an unknown density matrix of large size requires huge computational resources. The recent Factored Gradient Descent (FGD) algorithm and its variants achieved state-of-the-art performance since they could mitigate the dimensionality barrier by utilizing some of the underlying structures of the density matrix. Despite their theoretical guarantee of a linear convergence rate, the convergence in practical scenarios is still slow because the contracting factor of the FGD algorithms depends on the condition number κ of the ground truth state. Consequently, the total number of iterations can be as large as O(√κ ln(1/ε)) to achieve the estimation error ε. In this work, we derive a quantum state tomography scheme that improves the dependence on κ to the logarithmic scale; namely, our algorithm could achieve the approximation error ε in O(ln(1/κε)) steps. The improvement comes from the application of the non-convex Riemannian gradient descent (RGD). The contracting factor in our approach is thus a universal constant that is independent of the given state. Our theoretical results of extremely fast convergence and nearly optimal error bounds are corroborated by numerical results |
| Reference | https://arxiv.org/abs/2208.13492 |
| Personal information | |
| Video | Quantum state tomography via non-convex Riemannian gradient descent – YouTube |