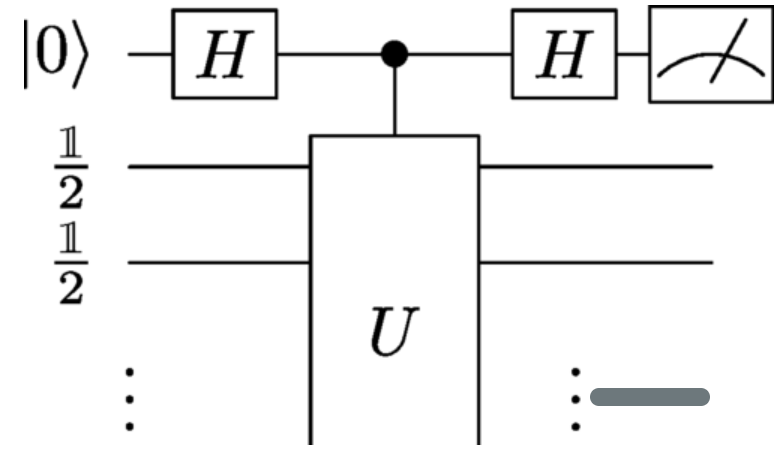
We describe a quantum algorithm to estimate the 𝛼-Renyi entropy of an unknown density matrix 𝜌∈ℂ𝑑×𝑑 for 𝛼≠1 by combining the recent technique of quantum singular value transformations with the method of estimating normalized traces in the one clean qubit model. We consider an oracular input model where the input state is prepared via a quantum oracle that outputs a purified version of the state, assumed to be nonsingular. Our method outputs an estimate of the 𝛼-Renyi entropy to additive precision 𝜀, using an expected total number 𝑂⁡(1(𝑥⁢𝜀)2) of independent applications of a quantum circuit which coherently queries the input unitary 𝑂⁡(1𝛿⁢log⁡𝑑𝜀) times, in each case measuring a single output qubit. Here 𝛿 is a lower cutoff on the smallest eigenvalue of 𝜌 and 𝑥=1𝑑⁢Tr⁡(𝜌𝛼). The expected number of measurements made in this method can be compared to results in the sample complexity model that generally require Θ⁡(𝑑2𝜀2) samples. Furthermore, we also show that multiplicative approximations can be obtained by iteratively using additive approximations, with an overhead logarithmic in the dimension 𝑑.