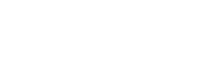Yuxuan Du, Yibo Yang, Dacheng Tao, and Min-Hsiu Hsieh
Abstract
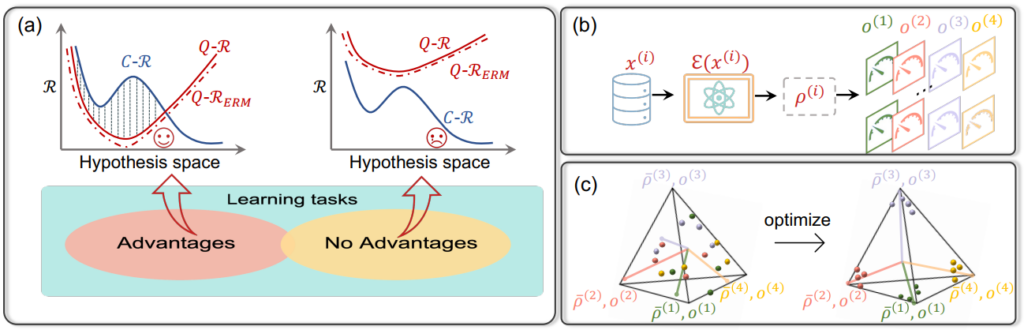
Quantum neural networks (QNNs) have become an important tool for understanding the physical world, but their advantages and limitations are not fully understood. Some QNNs with specific encoding methods can be efficiently simulated by classical surrogates, while others with quantum memory may perform better than classical classifiers. Here we systematically investigate the problem-dependent power of quantum neural classifiers (QCs) on multi-class classification tasks. Through the analysis of expected risk, a measure that weighs the training loss and the generalization error of a classifier jointly, we identify two key findings: first, the training loss dominates the power rather than the generalization ability; second, QCs undergo a U-shaped risk curve, in contrast to the double-descent risk curve of deep neural classifiers. We also reveal the intrinsic connection between optimal QCs and the Helstrom bound and the equiangular tight frame. Using these findings, we propose a method that . Numerical results demonstrate the effectiveness of our approach to explain the superiority of QCs over multilayer Perceptron on parity datasets and their limitations over convolutional neural networks on image datasets. Our work sheds light on the problem-dependent power of QNNs and offers a practical tool for evaluating their potential merit.