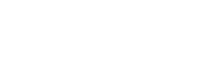Irit Dinur, Min-Hsiu Hsieh, Ting-Chun Lin, Thomas Vidick
STOC 2023, accpeted on Feb 06, 2023.
Abstract
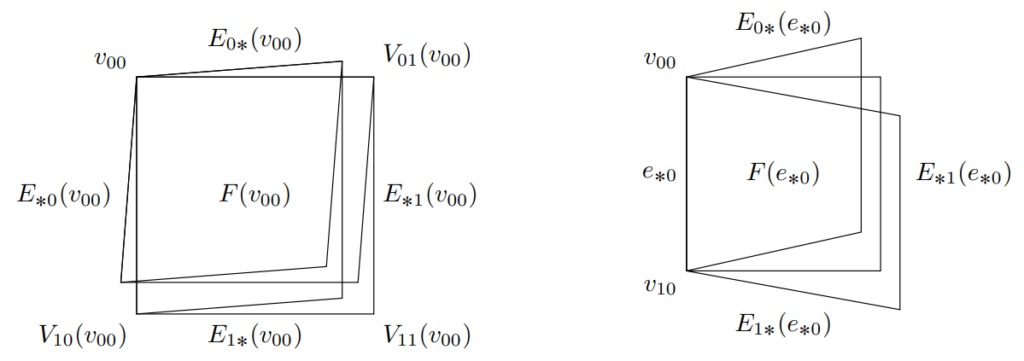
We construct a new explicit family of good quantum low-density parity-check codes which additionally have linear time decoders. Our codes are based on a three-term chain (Fm×m2)V−→δ0(Fm2)E−→δ1FF2 where V (X-checks) are the vertices, E (qubits) are the edges, and F (Z-checks) are the squares of a left-right Cayley complex, and where the maps are defined based on a pair of constant-size random codes CA,CB:Fm2→FΔ2 where Δ is the regularity of the underlying Cayley graphs.
One of the main ingredients in the analysis is a proof of an essentially-optimal robustness property for the tensor product of two random codes.
[Link]