Jihao Fan, Jun Li, Ya Wang, Yonghui Li, Min-Hsiu Hsieh, Jiangfeng Du
IEEE Transactions on Information Theory, vol. 69, no. 1, pp. 262-272, Jan. 2023
Abstract
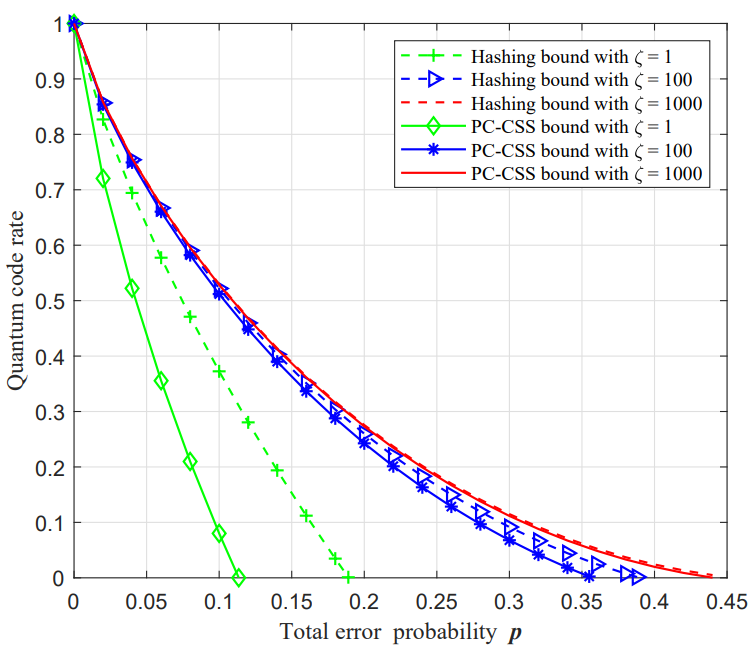
In this paper, we utilize a concatenation scheme to construct new families of quantum error correction codes achieving the quantum Gilbert-Varshamov (GV) bound asymptotically. Weconcatenate alternant codes with any linear code achievingthe classical GV bound to construct Calderbank-Shor-Steane (CSS) codes. We show that the concatenated code can achieve the quantum GV bound asymptotically and can approach the Hashing bound for asymmetric Pauli channels. By combing Steane’s enlargement construction of CSS codes, we derive a family of enlarged stabilizer codes achieving the quantum GV bound for enlarged CSS codes asymptotically. Asapplications, we derive two families of fast encodable and decodable CSS codes with parameters Q1=[[N,Ω(√N),Ω(√N)]] , and Q2=[[N,Ω(N/logN),Ω(N/logN)/Ω(logN)]] . We show that Q1 can be encoded very efficiently by circuits of size O(N) and depth O(√N) . For an input error syndrome, Q1 can correct any adversarial error of weight up to half the minimum distance bound in O(N) time. Q1 can also be decoded in parallel in O(√N) time by using O(√N) classical processors. For an input error syndrome, we proved that Q2 can correct a linear number of X -errors with high probability and an almost linear number of Z -errors in O(N) time. Moreover, Q2 can be decoded in parallel in O(log(N)) time by using O(N) classical processors.
[Link]