Abstract

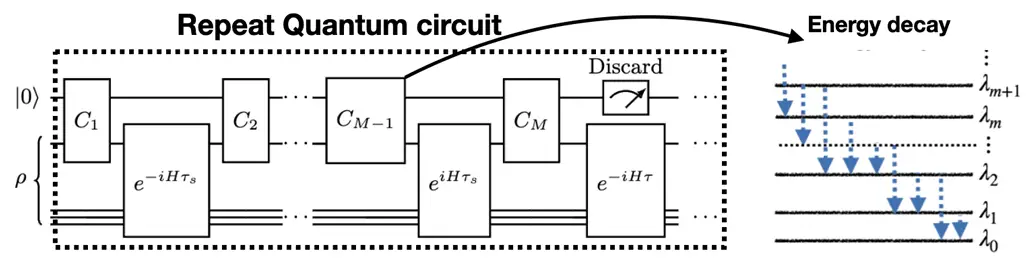
We present a polynomial-time classical algorithm for estimating expectation values of arbitrary observables on typical quantum circuits under any incoherent local noise, including non-unital or dephasing. Although previous research demonstrated that some carefully designed quantum circuits affected by non-unital noise cannot be efficiently simulated, we show that this does not apply to average-case circuits, as these can be efficiently simulated using Pauli-path methods. Specifically, we prove that, with high probability over the circuit gates choice, Pauli propagation algorithms with tailored truncation strategies achieve an inversely polynomially small simulation error. This result holds for arbitrary circuit topologies and for any local noise, under the assumption that the distribution of each circuit layer is invariant under single-qubit random gates. Under the same minimal assumptions, we also prove that most noisy circuits can be truncated to an effective logarithmic depth for the task of {estimating} expectation values of observables, thus generalizing prior results to a significantly broader class of circuit ensembles. We further numerically validate our algorithm with simulations on a 6×6 lattice of qubits under the effects of amplitude damping and dephasing noise, as well as real-time dynamics on an 11×11 lattice of qubits affected by amplitude damping.

Personal information

Armando Angrisani received his the Ph.D. degree in computer science from Sorbonne University, Paris, France, in 2023. Currently, he is a postdoctoral researcher in Zoë Holmes's group at the Swiss Federal Institute of Technology of Lausanne (EPFL), Switzerland. He is interested in the interplay between quantum information theory, quantum learning theory and classical algorithms for simulating quantum systems.