Jun Qi, Chao-Han Huck Yang, Pin-Yu Chen & Min-Hsiu Hsieh
npj Quantum Information volume 9, Article number: 4 (2023).
Abstract
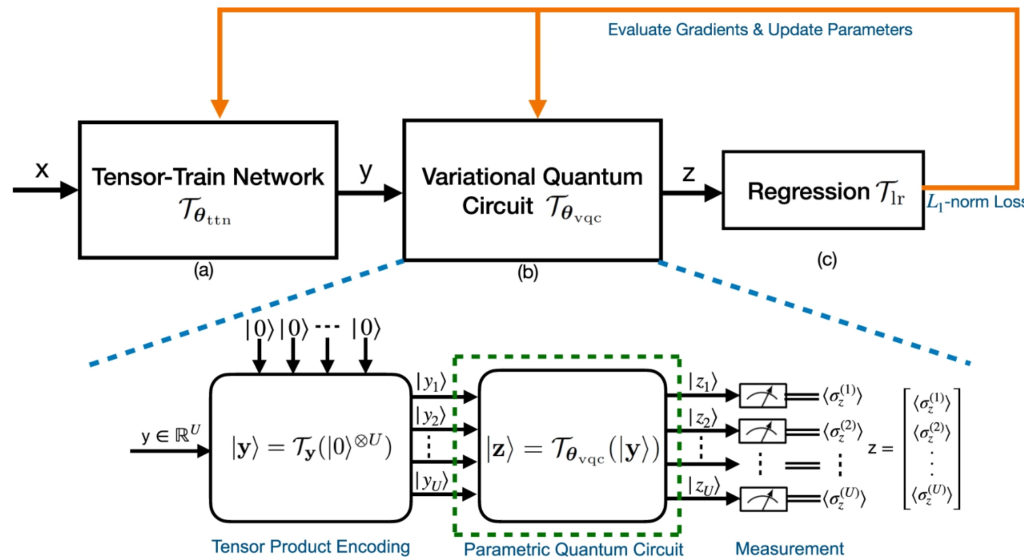
The noisy intermediate-scale quantum devices enable the implementation of the variational quantum circuit (VQC) for quantum neural networks (QNN). Although the VQC-based QNN has succeeded in many machine learning tasks, the representation and generalization powers of VQC still require further investigation, particularly when the dimensionality of classical inputs is concerned. In this work, we first put forth an end-to-end QNN, TTN-VQC, which consists of a quantum tensor network based on a tensor-train network (TTN) for dimensionality reduction and a VQC for functional regression. Then, we aim at the error performance analysis for the TTN-VQC in terms of representation and generalization powers. We also characterize the optimization properties of TTN-VQC by leveraging the Polyak-Lojasiewicz condition. Moreover, we conduct the experiments of functional regression on a handwritten digit classification dataset to justify our theoretical analysis.
[Link]