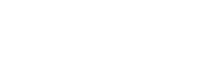Xu-Fei Yin, Yuxuan Du, Yue-Yang Fei, Rui Zhang, Li-Zheng Liu, Yingqiu Mao, Tongliang Liu, Min-Hsiu Hsieh, Li Li, Nai-Le Liu, Dacheng Tao, Yu-Ao Chen, and Jian-Wei Pan
Phys. Rev. Lett. 128, 110501 – Published 14 March 2022
ABSTRACT
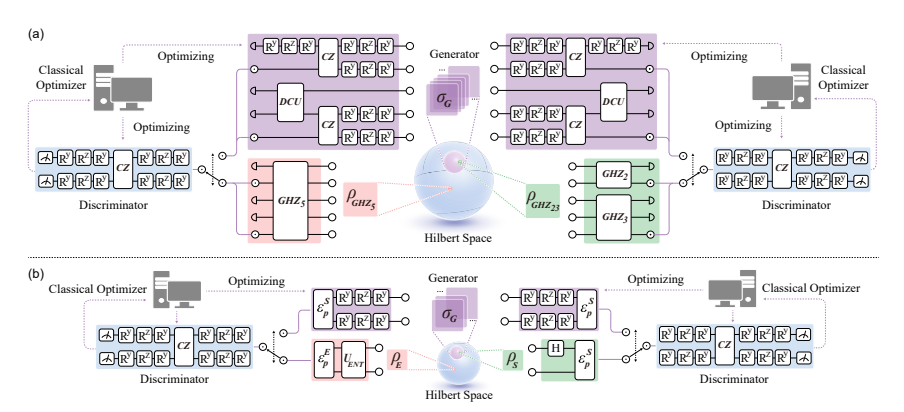
The recognition of entanglement states is a notoriously difficult problem when no prior information is available. Here, we propose an efficient quantum adversarial bipartite entanglement detection scheme to address this issue. Our proposal reformulates the bipartite entanglement detection as a two-player zero-sum game completed by parameterized quantum circuits, where a two-outcome measurement can be used to query a classical binary result about whether the input state is bipartite entangled or not. In principle, for an N-qubit quantum state, the runtime complexity of our proposal is O(poly(N)T) with T being the number of iterations. We experimentally implement our protocol on a linear optical network and exhibit its effectiveness to accomplish the bipartite entanglement detection for 5-qubit quantum pure states and 2-qubit quantum mixed states. Our work paves the way for using near-term quantum machines to tackle entanglement detection on multipartite entangled quantum systems.