Hao-Chung Cheng, Li Gao and Min-Hsiu Hsieh
communications in Mathematical Physics 390, pages 501–544 (2022)
ABSTRACT
R´enyi and Augustin information are generalizations of mutual information defined via the
R´enyi divergence, playing a significant role in evaluating the performance of information processing tasks
by virtue of its connection to the error exponent analysis. In quantum information theory, there are
three generalizations of the classical R´enyi divergence—the Petz’s, sandwiched, and log-Euclidean versions,
that possess meaningful operational interpretation. However, the associated quantum R´enyi and Augustin
information are much less explored compared with their classical counterpart, and lacking crucial properties
hinders applications of these quantities to error exponent analysis in the quantum regime.
The goal of this paper is to analyze fundamental properties of the R´enyi and Augustin information
from a noncommutative measure-theoretic perspective. Firstly, we prove the uniform equicontinuity for
all three quantum versions of R´enyi and Augustin information, and it hence yields the joint continuity of
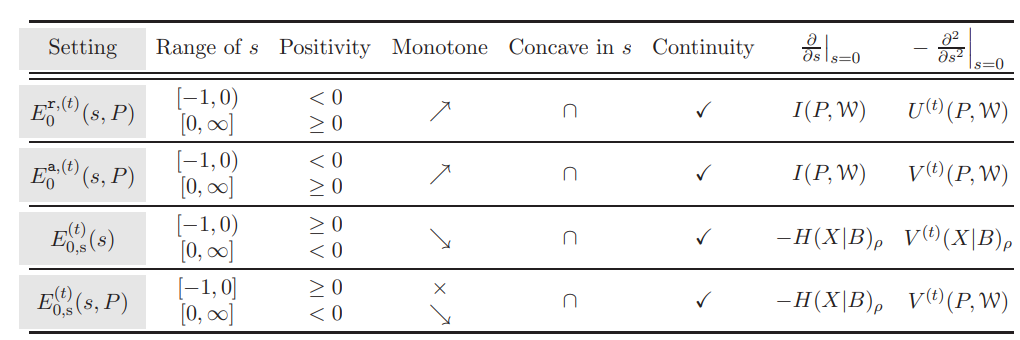
these quantities in order and prior input distributions. Secondly, we establish the concavity of the scaled
R´enyi and Augustin information in the region of s ∈ (−1, 0) for both Petz’s and the sandwiched versions.
This completes the open questions raised by Holevo [IEEE Trans. Inf. Theory, 46(6):2256–2261, 2000], and
Mosonyi and Ogawa [Commun. Math. Phys., 355(1):373–426, 2017]. For the applications, we show that
the strong converse exponent in classical-quantum channel coding satisfies a minimax identity, which means
that the strong converse exponent can be attained by the best constant composition code. The established
concavity is further employed to prove an entropic duality between classical data compression with quantum
side information and classical-quantum channel coding, and a Fenchel duality in joint source-channel coding
with quantum side information.