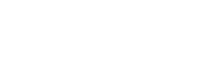Yuxuan Du, Min-Hsiu Hsieh, Tongliang Liu, Shan You, Dacheng Tao
PRX Quantum 2, 040337 – Published 17 November 2021 [arXiv]
Abstract
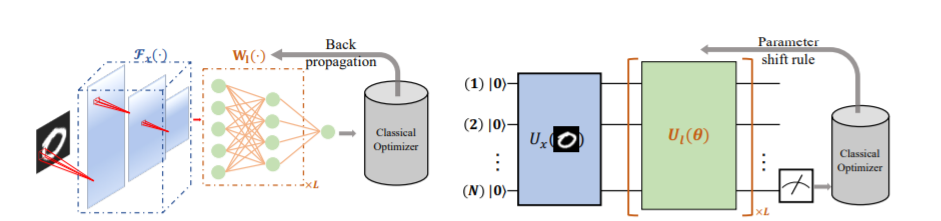
Quantum neural network (QNN), or equivalently, the parameterized quantum circuit (PQC) with a gradient-based classical optimizer, has been broadly applied to many experimental proposals for noisy intermediate-scale quantum (NISQ) devices. However, the learning capability of QNN remains largely unknown due to the nonconvex optimization landscape, the measurement error, and the unavoidable gate noise introduced by NISQ machines. In this study, we theoretically explore the learnability of QNN in the view of the trainability and generalization. Particularly, we derive the convergence performance of QNN under the NISQ setting, and identify classes of computationally hard concepts that can be efficiently learned by QNN. Our results demonstrate that large gate noise, few quantum measurements, and deep circuit depth will lead to poor convergence rates of QNN towards the empirical risk minimization. Moreover, we prove that any concept class, which is efficiently learnable by a quantum statistical query (QSQ) learning model, can also be efficiently learned by PQCs. Since the QSQ learning model can tackle certain problems such as parity learning with a runtime speedup, our result suggests that PQCs established on NISQ devices will retain the quantum advantage measured by generalization ability. Our work provides theoretical guidance for developing advanced QNNs and opens up avenues for exploring quantum advantages beyond hybrid quantum-classical learning protocols in the NISQ era.