Hayata Yamasaki, Madhav Krishnan Vijayan, Min-Hsiu Hsieh
Quantum 5, 480 (2021) [arXiv]
Abstract
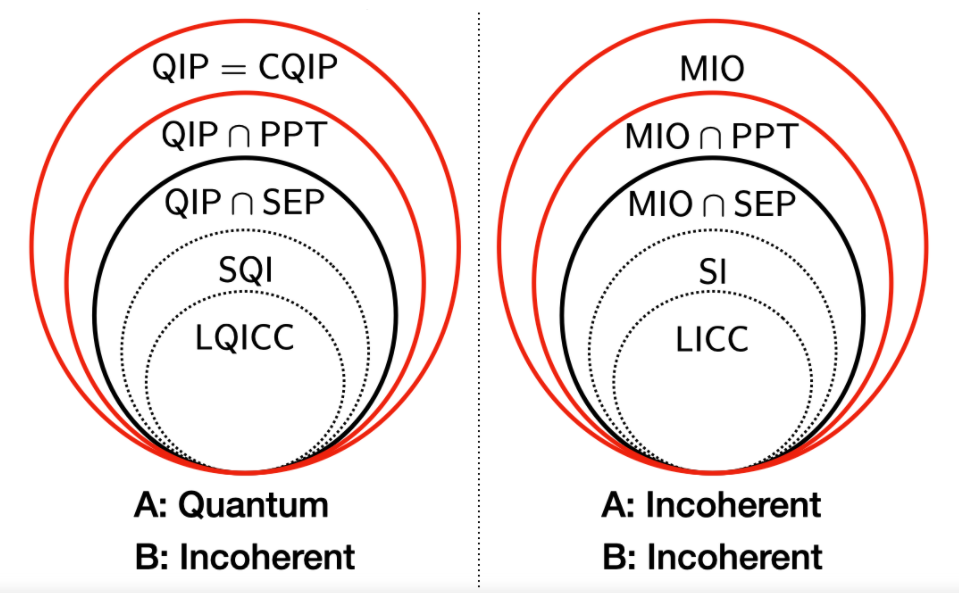
Quantum resource theory under different classes of quantum operations advances multiperspective understandings of inherent quantum-mechanical properties, such as quantum coherence and quantum entanglement. We establish hierarchies of different operations for manipulating coherence and entanglement in distributed settings, where at least one of the two spatially separated parties are restricted from generating coherence. In these settings, we introduce new classes of operations and also characterize those maximal, i.e.i.e., the resource-non-generating operations, progressing beyond existing studies on incoherent versions of local operations and classical communication and those of separable operations. The maximal operations admit a semidefinite-programming formulation useful for numerical algorithms, whereas the existing operations not. To establish the hierarchies, we prove a sequence of inclusion relations among the operations by clarifying tasks where separation of the operations appears. We also demonstrate an asymptotically non-surviving separation of the operations in the hierarchy in terms of performance of the task of assisted coherence distillation, where a separation in a one-shot scenario vanishes in the asymptotic limit. Our results serve as fundamental analytical and numerical tools to investigate interplay between coherence and entanglement under different operations in the resource theory.